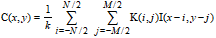
Linear convolution filters are based on a filter kernel that is convoluted with an image or in the one dimensional case a curve/profile. The filter kernel itself can be considered as an image (or in 1D as a curve) and also viewed as such. The SPIP program makes it easy to modify the filter kernel and display the kernel in 2D, 3D or for one-dimensional filter kernels as curves.
The Linear filter kernels provided are divided into the following categories:
- Smoothing (Low Pass, Mean, Gaussian)
- Sharpening (High Pass)
The mathematical description of a convolution with a filter kernel K of size N x M and an Image I is described below.
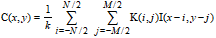
To avoid a general amplification of the data the sum of products are normally scaled by a factor 1/k , where k is the sum of the kernel coefficients.
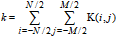
The simplest form of a convolution kernel is 1x1. Then the output data depends only on the value of the input data at the position (x,y) and the convolution becomes a gray-level transformation, which is also called mapping.