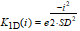 ,
,
Gaussian smoothing is often applied because the noise or the nature of the object observed might be of a Gaussian probable form. A two-dimensional Gaussian Kernel defined by its kernel size and standard deviation(s). Below are the formulas for 1D and 2D Gaussian filter shown SDx and SDy are the standard deviation for the x and y directions respectively.
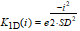 ,
,
The Gaussian filter works like the parametric LP filter but with the difference that larger kernels can be chosen.

Below a Gaussian filter is shown in 2D top view with horizontal and vertical cross sections and also in 3D view. The Gaussian function shown has a standard deviation of 10x10 and a kernel size of 35x35 pixels. Notice that a large part of the kernel for the y direction contains values very close to zero due to the low standard deviation in this direction. During the filtering process the filter kernel will be normalized so that it will not introduce a general amplification of the height values.

The size of the kernel should normally be selected large enough so that the kernel coefficients of the border rows and columns contribute very little to the sum of coefficients. By selecting a kernel size parameters six times the standard deviation the border parameters will be 1% or lower than the center parameter.
It is recommended to use the Auto Apply setting and having the Difference image included in the Output options such that the filter effect can be monitored in detail.
The standard deviation for a two-dimensional kernel is the radius in pixels containing 68% of the integrated magnitude of the coefficients. Increasing the standard deviation will increase the effective kernel size.
The Gaussian kernel can be used to perform an unsharp masking filter by subtracting the result from the original and can in this way serve as an ideal high pass filter. This is discussed in the "High Pass Filter" section.
A special implementation of the Gaussian filter is the ISO 11562 Gaussian profile filter; this filter is discussed in the ISO standard section. The shape of the filter is equal to the Gaussian filter described here, but the Gaussian ISO filter is defined by a cutoff wavelength measured in physical length units (e.g. nm or mm) determining which shorter waves should be reduced.
Below is seen a filtering example where the input image is shown upper left and the filter kernel upper right while the smoothening result is monitored lower left. The lower right image is difference image between input image and the filter result. While the smooth filter result reflects the long waves (waviness) the difference image reflects the short waves of the image.
