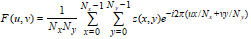Fourier analysis

The Fourier transform is a powerful tool for image analysis. This is true in particular for analysis of repeated patterns such as pitch standards and molecular or atomic structures. Fourier images reflect repeated patterns as narrow peaks, the co-ordinates of which describe their periodicity and direction. Such peaks are easy to detect by image processing without any pre-knowledge of the features form or periodicity. Furthermore, the repeat distances can be measured very accurately by determining the Fourier peak co-ordinates at sub-pixel level.

The discrete Fourier transform is calculated by the formula:

Where Nx, Ny are the number of pixels in the x,y directions and u,v the discrete Fourier indexes =0,1,2,..Nx-1 and v = 0,1,2..Ny-1. The Fourier transform can also be regarded as a sum of sinusoidal functions, each described by a frequency, amplitude and a phase.

The inverse transform, which, for example, may be applied after filtration where, for example, unwanted Fourier components are set to zero, has a similar form:

The number of computational operations can be reduced dramatically by Fast Fourier Transform (FFT) algorithms that break the calculation down to a sequence of smaller Fourier transforms. The highest efficiency is obtained when the side lengths Nx and Ny are powers of 2. Thus, typical images are 256 ´ 256 or 512 ´ 512 pixels. The chosen size is a compromise between a high pixel density and the costs in form of extra acquisition time, storage demands and calculation time.

The Fourier transform can be visualized by its amplitude spectrum, which contains the absolute values of the complex Fourier components:

where R and I denote the real and imaginary parts respectively.

The phase information is rarely used but preserved in case inverse transformations have to be applied after exclusion of some Fourier components. To enhance the contrast of weaker components a square root function or logarithmic function may be applied to the amplitude values. Likewise, more dominant components may appear with even higher contrast when the amplitude values are squared. Contrast changes by color manipulation may also be a valuable technique to reveal weak Fourier components.