Lateral Linearity Analysis

This advanced process can be started directly by pushing the associated key in the Analyze > Calibration & FFT ribbon pane:

From the detected lattice structure, we can predict the position of repeated features by knowing the position of a single feature belonging to the lattice.

We therefore select a single feature (template) representative of the lattice and by cross correlation we find the position of the other matching features.

If the Inspection image is active it will define the template which has to be recognized otherwise SPIP automatically finds a suitable template based on a detected unit cell.

The positions are identical to the peaks in the cross correlation function, which we estimate at sub-pixel level by parabolic fits. These positions are compared with the predictions based on the unit cell vectors and we calculate a prediction error vector ek,l:

where 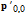is the vector pointing to the highest peak in the cross correlation function and 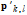the pointing vectors to the peaks in the cross correlation function that comes closest to

.

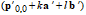The integers k,l are found so that ek,l is minimized.

The prediction error, ek,l, typically reflects non-equidistant sampling during scanning. However, imperfections of the sample or environmental conditions might also be reflected in the result.

Keeping k,l fixed it is possible to adjust the unit cell vectors a',b' by minimizing the mean position error:

where M is the number of peak vectors in the cross correlation image. We can thereby find an alternative calculation of the unit cell that can be compared with the one calculated from the Fourier domain. Eu also serves as a measure of the non-linearity; the smaller it is the better.

We can visualize the prediction errors for the x, y co-ordinates of ek,l independently as function of their x, y co-ordinates peak position co-ordinates of 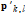, see d,e, and it is possible to estimate polynomial fits to the data and obtain correction functions. From the curve describing the x-co-ordinate error, 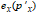we calculate the physical scanning co-ordinate:

To resample the image at equidistantly separated points a model that describes the observed co-ordinates as function of the physical co-ordinates can be applied. The observed 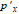co-ordinates can be modeled by a function of the physical positions 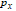by a least mean square polynomial fit

where N is the polynomial degree and the an coefficients found by minimizing the error function Ex:

Here the summation goes over all detected peaks in the cross correlation function.