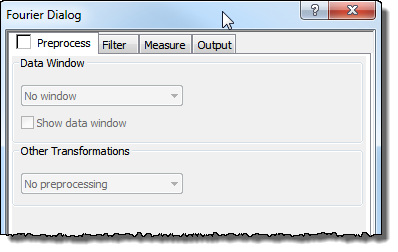
The Fourier Dialog offers two preprocessing techniques, which can be applied to an image before the Fourier Transform is performed, these are:
Data Window: mostly used for lowering border effects and improving measurement capabilities
Other Transformations: used for contrast enhancement

The optional Data Windows are used for minimizing an effect called spectral leakage and improving the measurement capabilities.
Discrete Fourier algorithms are created on the assumption that the input data set (image) contains an integer number of periods of an infinite number of periods. This is seldom the case and might therefore lead to undesired effects in the Fourier output. For example a curve or image dominated by a slope will in its infinite version be seen as a saw-tooth structure. As the Fourier Transformed data consist of a series of cosine functions each defined by a magnitude and phase it requires the use of higher harmonic cosine functions to describe a saw tooth structure. The resulting Fourier image will therefore contain components that are associated with the discontinuity created when repeating the images. This effect is called spectral leakage and is typically observed as stripes along the x and y axes with a magnitude that decreases as a sin(x)/x function.
The spectral leakage can have a negative effect on measurements performed in the Fourier Image and can make it more difficult to evaluate the more interesting Fourier structure.
To lower this spectral leakage effect Data Windows that lower the magnitude of the border data can be applied. The side effect of the Data Windows is that the Fourier Components very next to the true Fourier peaks (Main lobe) will appear higher while the spectral leakage components further away (the side lobes) will appear smaller.
It is also worth noting that a proper plane correction of the images can reduce the spectral leakage phenomenon dramatically.
Below is shown how proper plane correction and windowing can improve the quality of a Fourier image.
The Fourier Image is scaled by a double square root to enhance the contrast of the weaker components.
|
Tilted Image |
Fourier of Tilted Image, no preprocessing |
|
Data Window (Hanning) |
Fourier after applying Hanning data window |
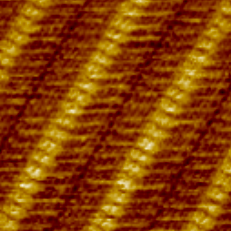
Plane Corrected Image |
|
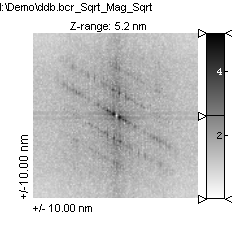
Fourier of plane corrected image
|
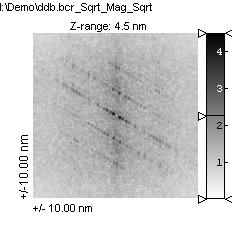
Fourier after applying data window |
SPIP offers the following Data Windows, which can be displayed by setting Show Data window on in the Output:
The data windows are multiplied to the image data before the Fourier Transform is performed and if an Inverse transform has to be carried in combination with Fourier Filtering it is therefore necessary to divide the Inverse Fourier result with the applied window. This requires that all window data contain non-zero values and we have therefore slightly modified the Data Windows so that no values are smaller than 0.001.
However, in combination with inverse filtering the best results are achieved when not applying data windows.
SPIP currently contains one other preprocessing transformation, which is at logarithmic function. This function can in combination with low pass filtering perform a so-called "Homomorphic Filtering" which can compress the brightness/height range and enhance the contrast at the same time. To perform Homomorphic Filtering follow these three steps: