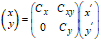Lateral Calibration by Quadratic Unit Cells

The method used for calibration by quadratic unit cells has been described in a paper [46] where the essence is given here.

To describe the correspondence between the observed surface lattice and the real physical lattice, we use the transformation matrix. Here we will ignore non-linearity and the influence from the z-axis. We arrange the co-ordinate system of the uncorrected and the correct co-ordinate systems so that their x-axes are parallel.

Where Cx, C_y and Cxy are the unknown correction parameters to be estimated. If the scanned x- and y-axes are perpendicular, then Cxy equals zero and Cx,Cy are the scale factors for the x- and the y-directions respectively, i.e.,

.

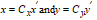
Cxy describes the coupling between the x and y axes, i.e. how much the scanner moves in the x-direction when stepping in the y-direction. The angle 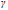between the scanned x-axis and the scanned y-axis is given by

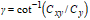and the angular distortion (gamma error)

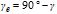
When using a calibration standard with square unit cells described by a repeat distance, L, then based on the observed unit cell vectors

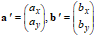
and the reference valuelwe can find an analytical solution for the three unknown correction parameters:

Off-line correction of images can be performed by re-sampling at equidistant (x',y') positions.