The MUFU Method and Parameters

The MUFU method is not an ISO standard but a methodology developed by The Technical University of Denmark and Image Metrology [27] for characterizing periodic plateau-valley type surfaces (MUFU profiles), for example generated by turning, and followed by partial grinding or polishing [26]. The aim with this method is to be able to evaluate the micro roughness and curvature of the plateaus, quantify the volume of the valleys and the angles of the profile at the plateau valley intersections etc.

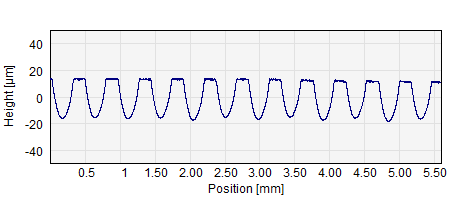
Example of a plateau-valley profile – which we call a MUFU profile

The Roughness Profile

In the MUFU method the roughness profile is generated by applying a seeded robust Gaussian regression filter on the Primary Profile. The filter has the cut-off wavelength given in the Roughness Analysis pane. The filter line is subtracted from the Primary Profile in order to generate the Roughness profile and serves as reference line for the roughness calculations. The filter line is displayed in the Primary profile.

As the filter line becomes the reference line for the Roughness Profile it is extremely important to ensure that the Plateaus have been successfully placed around Z=0. If this is not the case it is necessary to change the filter settings.

Seeded Gaussian regression filtering

There are two filters: A seeded 0th order robust Gaussian regression filter (RGR0) and a seeded 2nd order robust Gaussian regression filter (RGR2).

The Gaussian weighting function S(x) for the 0th order filter (RGR0) is a plain ISO 11562 Gaussian envelope, see Filters in Users Guide. The Gaussian weighting function S(x) for the 2nd order filter (RGR2) is slightly modified as described in the ISO 16610-31:2009 standard [30]. The 2nd order filter (RGR2) can follow form or waviness components by approximating a 2nd order polynomial curve to the weighted profile and thereby also takes care of end effects (run-in and run-out). This filter is, however, computationally considerably slower than the 0th order filter.

The filter mean line w(x) is calculated by minimizing the equations below [33]. ρ(r) is the error metric function of the estimated residuals.

0’th order regression minimization problem:

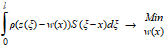
2nd order regression minimization problem:

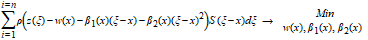
The filter equations are solved iteratively [28, 29, 30, 31, 32, 33, 34] using the (non-linear) Tukey estimator’s re-weighting function:

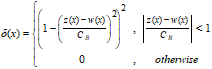
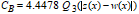
The threshold value C_B is calculated using the upper quartile, Q3, of the residuals [28, 27], instead of the median (MAD), though the median is more common and is the default according to the ISO 16610:31 standard [30].

Besides using the upper quartile for the threshold value CB the difference to the robust Gaussian regression method described in the ISO 16610-31 standard is that the first step of the iteration is substituted with a morphological closing filter as described in the ISO 16610-41:2006 [35]. standard. Both of these differences improve the filter’s ability to follow the plateaus.

As shown in the figure below C_Bis calculated for every iteration. Thereafter the weights are calculated, and the Gaussian equation for that iteration is solved. This is repeated until the relative change in C_B falls below e = 0.001.

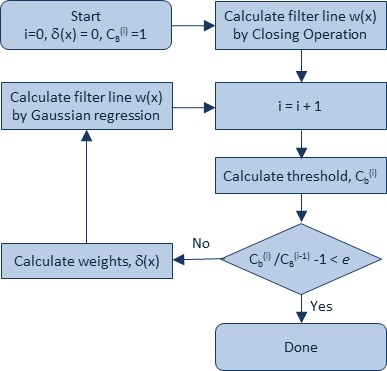
Flow chart of the robust Gaussian regression filtering algorithm.

Closing Filter

The closing filter used here is using a circular disc as the structuring element [35]. The disc radius is given by the Cut-Off Wavelength, λc, multiplied by the Closing Cut-Off Ratio, both entered by the user in the Roughness Pane.

A morphological closing filter is the result of applying a morphological dilation on the result of which morphological erosion is performed. The principle of dilation and erosion is shown in the figure below.

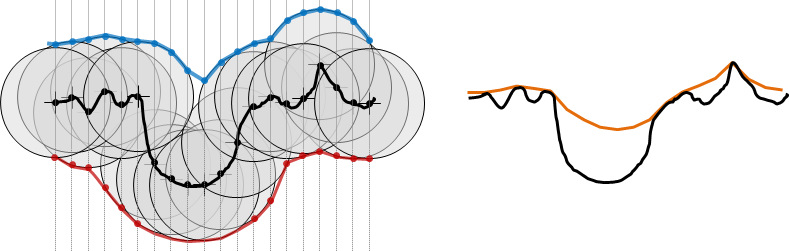
Dilation and erosion are performed by placing a disc in every point of the profile. The dilated curve (blue) consists of the maximum Z value of all circles for each point in the profile. The eroded (red) curve consists of all Z minima derived the same way. Closing is performed by applying erosion after dilation (orange curve to the right). Closing suppresses valleys when the disc radius is sufficiently large.

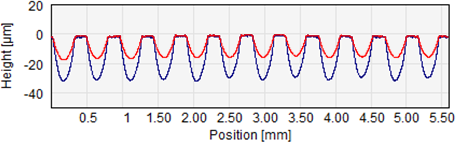
Result of applying a morphological closing operation with a disc radius of 0.8 mm on a MUFU plateau/valley profile. It is obvious that choosing a disc with a lager radius, i.e. increasing the Closing Cut-Off Ratio would give abetter valley suppression.

Feature separation

Plateaus are separated from valleys by the following procedure [27]. Features are detected within the Evaluation Length, given by the cut-off wavelength multiplied with the specified Number of Cut-Offs in the Roughness Analysis pane in the same way as for the ISO 4287 standard.

A height threshold level is calculated by finding the “knee” in the Material Probability Curve. First the Material Probability (MP) Curve is normalized so that the X and Y range becomes square. Then a line is drawn from the left most point to the right most point. The ordinate value in the un-normalized curve corresponding to the point in the normalized curve which has the largest outward distance from this line is the plateau valley threshold level – in the following denoted the upper threshold.

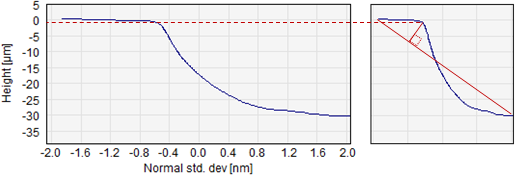
Material Probability Curve, original (left) and normalized (right) with indication on how to find the upper threshold level.

Segmenting the profile at this height level may, however, result in over segmentation because there may be local dips or valleys inside plateaus. Therefore, the profile is first thresholded at a lower level where after the sides of the resulting “plateaus” are removed up to the upper threshold level. The lower threshold is chosen as

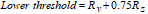
where R_v and R_z are calculated on the MUFU Roughness Curve according to the ISO 4287 standard.

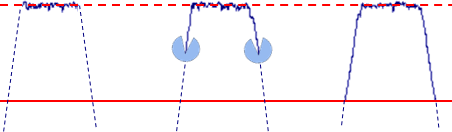
In order to avoid splitting plateaus at small local valleys the profile is first thresholded at a lower level where after further points are removed until the upper threshold is reached, thereby defining the intersection between neighboring plateaus and valleys.

MUFU Parameters

All MUFU parameters and curves are evaluated for the number of consecutive complete peak/valley pairs within the Evaluation Length. Thus the total distance spanned by the plateau/valley pairs will almost always be shorter than the Evaluation Length.

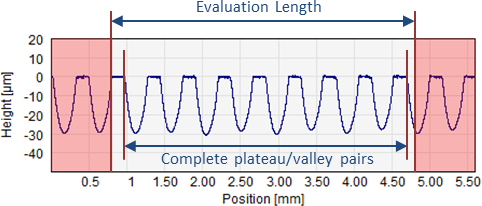
For all parameter calculations only complete plateau / valley pairs are included

Rn: Number of plateau/valley pairs
The number of complete plateau/valley pairs inside the Evaluation Length
Rw: Mean width of plateau/valley pairs
The average of the widths of all complete plateau / valley pairs inside the Evaluation Length.
Rpp: Plateau percentage (bearing area ratio)
The total length of plateaus divided by the total length, LPV, of all plateau/valley pairs, in percent.
Rpa: Arithmetic mean deviation of plateaus
Where np is the total number of points inside plateaus and Zi is the height value at point i.
Rpq: Root mean square deviation of the plateaus
Where np is the total number of points inside plateaus and Zi is the height value at point i.
Rvt: Equivalent mean film thickness of valley volume
The thickness of the lubricant retained in the valleys if it was distributed on a flat surface with the same dimensions as the plateau/valley surface. Where n is the total number of points inside the total plateau valley length and nv is the total number of points inside the valleys. The reference level for valley volume is the upper threshold level, UT, and not the filter line as for the plateau parameters because this is more robust.
Rvc: Mean radius of curvature of the bottom of valleys
A parabola is fitted to each valley and the radius of curvature is calculated. Rvc is the average of all calculated valley curvatures. Where aj is coefficient of the 2nd order term in the parabolic fit (ajx2 + bjx + cj) for valley number j.
Rvl: Mean take-off angle of the left side of valleys near the plateaus
For each valley a parabola is fitted in the 0-10 % range of valley points (the leftmost 10%). The slope (in degrees) of the parabola at the upper threshold level is calculated and averaged over all valleys, see illustration for Rvc. Rvl is a positive number.
Rvr: Mean take-off angle of the right side of valleys near the plateaus
For each valley a parabola is fitted in the 90-100 % range of valley points (the rightmost 10%). The slope (in degrees) of the parabola at the upper threshold level is calculated and averaged over all valleys, see illustration for Rvc. Rvr is a positive number.
Rpc: Mean plateau radius of curvature
A parabola is fitted to each plateau and the radius of curvature is calculated. Rpc is the average of all calculated plateau curvatures. Where aj is coefficient of the 2nd order term in the parabolic fit (ajx2 + bjx + cj) for plateau number j.
Rpac: Arithmetic mean deviation of plateaus after curvature removal
This is the same as Rpa but calculated after removing the curvature of all plateaus by subtracting the individually fitted parabola (see Rpc) for each plateau.
Rpqc: Root mean square deviation of the plateaus after curvature removal
This is the same as Rpq but calculated after removing the curvature of all plateaus by subtracting the individually fitted parabola (see Rpc) for each plateau.

MUFU graphs

In addition to the graphs available for all standards the MUFU method also offers to display the separated plateaus and the separated valleys independently. These are mostly provided for instructive purposes but also makes it clear exactly which part of the profile has been used for the MUFU parameter calculations and which parts are valleys and which parts are plateaus.

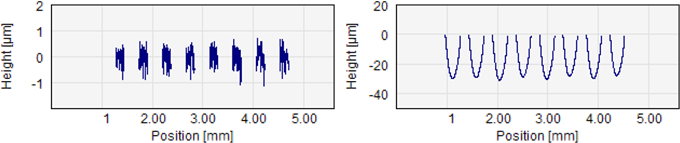
Separate plateau/valley graphs. Note that the height scale is different on the two shown graphs.